1007. Minimum Domino Rotations For Equal Row

Problem

Tags: Array, Greedy

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the i^th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i^th domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Example 1:

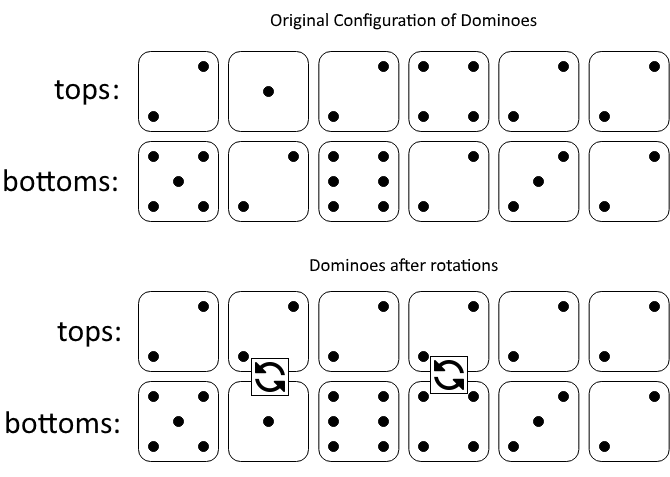
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

• 2 <= tops.length <= 2 * 10^4
• bottoms.length == tops.length
• 1 <= tops[i], bottoms[i] <= 6

Code

C

// 1007. Minimum Domino Rotations For Equal Row (9/28/54185)
// Runtime: 116 ms (91.89%) Memory: 11.40 MB (45.95%) 

#define MAX(a, b) ((a > b) ? a : b)

int minDominoRotations (int tops[], int tops_size, int bottoms[], int bottoms_size) {
    uint16_t both[7] = { 0 };
    uint16_t only_tops[7] = { 0 };
    uint16_t only_bottoms[7] = { 0 };
    
    for (int i = 0; i < tops_size; i++) {
        if (tops[i] == bottoms[i]) {
            both[tops[i]]++;
        } else {
            only_tops[tops[i]]++;
            only_bottoms[bottoms[i]]++;
        }
    }
    
    for (int i = 1; i < 7; i++) {
        if (only_tops[i] + only_bottoms[i] + both[i] == tops_size) {
            return tops_size - both[i] - MAX(only_tops[i], only_bottoms[i]);
        }
    }
    
    return -1;
}