1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

Problem

Tags: Array, Greedy, Sorting

You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:

• horizontalCuts[i] is the distance from the top of the rectangular cake to the i^th horizontal cut and similarly, and
• verticalCuts[j] is the distance from the left of the rectangular cake to the j^th vertical cut.

Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 10^9 + 7.

Example 1:

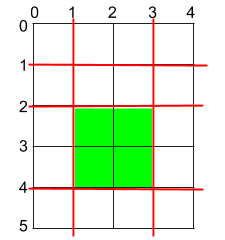
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
Output: 4 
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.

Example 2:

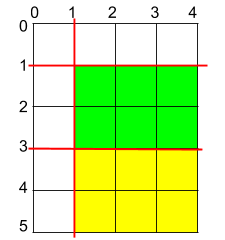
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
Output: 6
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.

Example 3:

Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
Output: 9

Constraints:

• 2 <= h, w <= 10^9
• 1 <= horizontalCuts.length <= min(h - 1, 10^5)
• 1 <= verticalCuts.length <= min(w - 1, 10^5)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• All the elements in horizontalCuts are distinct.
• All the elements in verticalCuts are distinct.

Code

C

// 1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts (4/23/53956)
// Runtime: 56 ms (75.00%) Memory: 12.24 MB (50.00%) 

int compare (const int *a, const int *b) {
    return (*a - *b);
}

int maxArea(int h, int w, int horizontalCuts[], int horizontalCutsSize, int verticalCuts[], int verticalCutsSize){
    // 先把切割線都做遞增排序
    qsort(horizontalCuts, horizontalCutsSize, sizeof(int), compare);
    qsort(verticalCuts, verticalCutsSize, sizeof(int), compare);

    // 紀錄最大高度以及最大寬度，初始值設為第一條切割線到相鄰邊界的距離
    int64_t max_height = horizontalCuts[0], max_width = verticalCuts[0];

    // 逐步看兩相鄰切割線距離，找最大高度
    for(int i = 1; i < horizontalCutsSize; i++) {
        int64_t height = horizontalCuts[i] - horizontalCuts[i - 1];
        max_height = height > max_height ? height : max_height;
    }
    // 也要看看最後一條切割線到相鄰邊界的距離
    int64_t height = h - horizontalCuts[horizontalCutsSize - 1];
    max_height = height > max_height ? height : max_height;
    
    // 逐步看兩相鄰切割線距離，找最大寬度
    for(int i = 1; i < verticalCutsSize; i++) {
        int64_t width = verticalCuts[i] - verticalCuts[i - 1];
        max_width = width > max_width ? width : max_width;
    }
    // 看看最後一條切割線到相鄰邊界的距離
    int64_t width = w - verticalCuts[verticalCutsSize - 1];
    max_width = width > max_width ? width : max_width;
    
    // 輸出最大塊面積
    return (int)((max_height * max_width) % (int64_t)1000000007);
}

JS

// 1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts (1/9/53394)
// Runtime: 140 ms (79.22%) Memory: 48.12 MB (94.81%) 

/**
 * @param {number} h
 * @param {number} w
 * @param {number[]} horizontalCuts
 * @param {number[]} verticalCuts
 * @return {number}
 */
var maxArea = function(h, w, horizontalCuts, verticalCuts) {
    verticalCuts.sort((a,b) => a - b);
    horizontalCuts.sort((a,b) => a - b);
    console.log(verticalCuts[0], verticalCuts[verticalCuts.length - 1]);
    console.log(horizontalCuts[0], horizontalCuts[horizontalCuts.length - 1]);
    
    let max_height = horizontalCuts[0], max_width = verticalCuts[0];
    for(let i = 1; i < horizontalCuts.length; i++) {
        let height = horizontalCuts[i] - horizontalCuts[i - 1];
        max_height = height > max_height ? height : max_height;
    }
    let height = h - horizontalCuts[horizontalCuts.length - 1];
    max_height = height > max_height ? height : max_height;
    
    for(let i = 1; i < verticalCuts.length; i++) {
        let width = verticalCuts[i] - verticalCuts[i - 1];
        max_width = width > max_width ? width : max_width;
    }
    let width = w - verticalCuts[verticalCuts.length - 1];
    max_width = width > max_width ? width : max_width;
    
    return (max_height * max_width) % (1e9 + 7);
};