363. Max Sum of Rectangle No Larger Than K

Problem

Tags: Array, Binary Search, Dynamic Programming, Matrix, Ordered Set

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

Example 1:

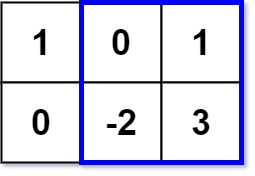
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -100 <= matrix[i][j] <= 100
• -10^5 <= k <= 10^5

Follow up: What if the number of rows is much larger than the number of columns?

Code

CPP

// 363. Max Sum of Rectangle No Larger Than K (9/26/53474)
// Runtime: 1088 ms (71.27%) Memory: 294.13 MB (11.84%) 

class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        const int m = matrix.size();
        const int n = matrix[0].size();

        int ans = INT_MIN;

        for (int baseCol = 0; baseCol < n; ++baseCol) {
          // sums[i] := sum(matrix[i][baseCol..j])
          vector<int> sums(m, 0);
          for (int j = baseCol; j < n; ++j) {
            for (int i = 0; i < m; ++i)
              sums[i] += matrix[i][j];
            // find the max subarray no more than k
            set<int> accumulate{0};
            int prefix = 0;
            for (const int sum : sums) {
              prefix += sum;
              const auto it = accumulate.lower_bound(prefix - k);
              if (it != cend(accumulate))
                ans = max(ans, prefix - *it);
              accumulate.insert(prefix);
            }
          }
        }

        return ans;
    }
};