576. Out of Boundary Paths

Problem

Tags: Dynamic Programming

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 10^9 + 7.

Example 1:

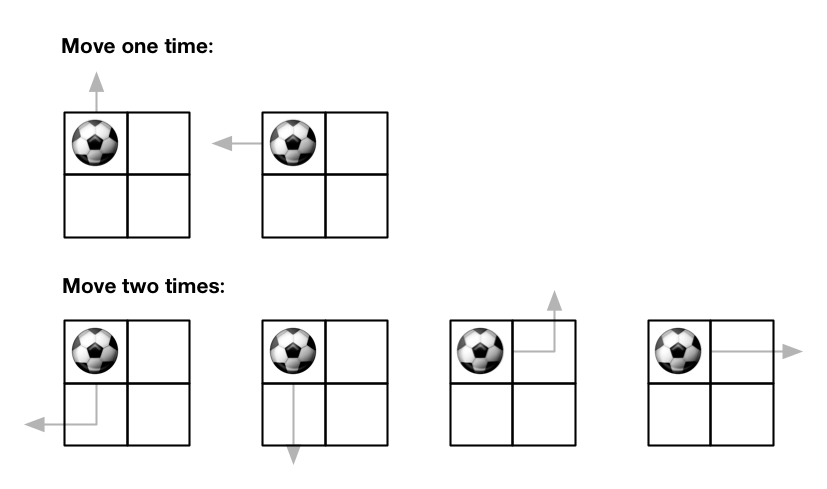
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6

Example 2:

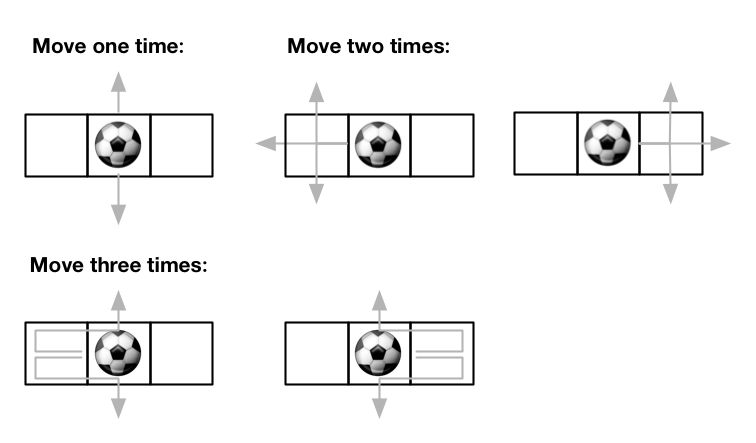
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12

Constraints:

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow < m
• 0 <= startColumn < n

Code

JS

// 576. Out of Boundary Paths (10/26/53449)
// Runtime: 100 ms (88.89%) Memory: 46.43 MB (85.19%) 

/**
 * @param {number} m
 * @param {number} n
 * @param {number} maxMove
 * @param {number} startRow
 * @param {number} startColumn
 * @return {number}
 */
var findPaths = function(m, n, maxMove, startRow, startColumn) {
    let dp = [];
    for(let move = 0; move <= maxMove; move++) {
        dp.push([]);
        for(let row = 0; row < m; row++) {
            dp[move].push([]);
            for(let col = 0; col < n; col++) {
                dp[move][row].push(0);
            }
        }
    }
    
    for(let move = 1; move <= maxMove; move++) {
        for(let row = 0; row < m; row++) {
            for(let col = 0; col < n; col++) {
                let up = (row !== 0) ? dp[move-1][row-1][col] : 1;
                let down = (row !== m-1) ? dp[move-1][row+1][col] : 1;
                let left = (col !== 0) ? dp[move-1][row][col-1] : 1;
                let right = (col !== n-1) ? dp[move-1][row][col+1] : 1;
                let sum = up + down + left + right;
                dp[move][row][col] = sum % (1e9+7);
            }
        }
    }
    
    return dp[maxMove][startRow][startColumn];
};